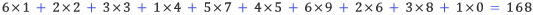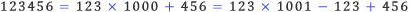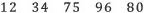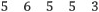[스크랩] 수학이야기 - 7의 배수 판정법

초등학교에서 분수를 배울 때를 생각해 보면, 분수의 계산 결과는 언제나 약분하여 간단한 모양이 되도록 한다. 분수를 약분하려면, 분모와 분자의 수가 어떤 수의 배수인지를 판정하는 과정이 필요하다. 2의 배수부터 9의 배수까지 간단한 판정법이 알려져 있지만, 이상하게도 7의 배수 판정법은 별로 알려진 것이 없다. 7을 제외한 2에서 9까지 배수판정법을 간단히 정리해보고, 7의 배수판정법을 집중적으로 알아보기로 한다.     배수 판정법 7을 제외한 2, 3, 4, 5, 6, 8, 9의 배수 판정법은 다음과 같다.                     2의 배수 판정법 : 끝자리가 0, 2, 4, 6, 8이면 원래 수는 2의 배수이다.                   3의 배수 판정법 : 각 자리 수의 합이 3의 배수이면 원래 수도 3의 배수이다.                   4의 배수 판정법 : 끝 두 자리 수가 4의 배수이면 원래 수도 4의 배수이다.                   5의 배수 판정법 : 끝자리가 0 또는 5이면 원래 수는 5의 배수이다.                   6의 배수 판정법 : 2의 배수이면서 동시에 3의 배수이면 원래 수는 6의 배수이다.                   8의 배수 판정법 : 끝 세 자리 수가 8의 배수이면 원래 수도 8의 배수이다.                   9의 배수 판정법 : 각 자리 수의 합이 9의 배수이면 원래 수도 9의 배수이다.   예를 들어, 1234759680은 끝 세 자리 수 680이 8의 배수이므로 원래 수도 8의 배수이고, 각 자리 수의 합이 45이므로 원래 수도 9의 배수이다. 따라서 이 수는 2, 3, 4, 6, 8, 9의 배수가 됨을 알 수 있다. 끝자리 수가 0이므로 5의 배수인 것도 분명하다. 그렇다면 7은 어떨까? 이 수가 7의 배수인지 아닌지 직접 나누어 보지 않고 알 수 있는 방법은 없을까?   7의 배수 판정법(1) 과거의 방법 다른 수의 판정법과 달리 7의 배수 판정법은 여러 가지 다양한 방법이 개발되어 있지만, 대부분 그리 간단하지 않아서 직접 나누는 것과 큰 차이가 없는 경우가 많다. 가장 오래된 판정법 가운데 하나는 다음과 같다.                     1. 일의 자리부터 시작하여 커지는 방향으로 각 자리 수에 1, 3, 2, 6, 4, 5를 반복하여 곱한다.                   2. 위에서 곱한 수들을 모두 더한다.                    3. 위의 합이 7의 배수이면 원래 수도 7의 배수이다.   예를 들어, 앞서 보았던 1234759680에 이 판정법을 적용하면 다음과 같다.     168이 7의 배수이므로 이 수는 7의 배수이다. 이 방법은 1, 10, 100, 1000, …을 7로 나눈 나머지를 이용하는 방식으로, 어떤 수의 배수 판정법이라도 비슷한 방법으로 만들어낼 수 있는 장점이 있지만, 여섯 개의 숫자 1, 3, 2, 6, 4, 5를 외우느니 차라리 7로 일일이 나누는 편이 차라리 쉬울 것 같다.     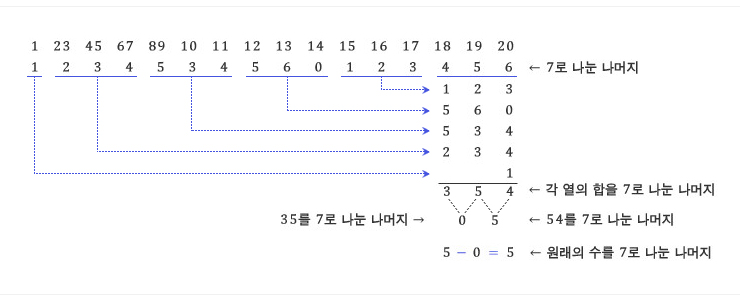7의 배수 판정법(2) 스펜스의 방법 비교적 간단하면서도 그런대로 효과적인 방법은 일의 자리 수를 두 배 하여 일의 자리를 제외한 나머지 수에 뺀 결과가 7의 배수인지를 살펴보는 것이다. 예를 들어 469의 일의 자리 수 9를 두 배 한 18을 46에서 빼면 46-18 = 28이고, 이것은 7의 배수이므로 원래의 수 469도 7의 배수이다. 두 배 해서 빼는 대신, 다섯 배 하여 더하여도 된다. 이 과정을 반복하면 큰 수도 7의 배수인지 아닌지 판정할 수 있다. 다음은 1234759680에 이 판정법을 적용한 것이다.

 

 

최종 결과인 0이 7의 배수이므로 원래의 수도 7의 배수가 된다. 이 방법을 발견한 사람의 이름을 따 “스펜스(Spence)의 방법”으로도 불리는 이 판정법은 간단하기는 하지만 다른 수의 배수 판정법에 비해 꽤 많은 계산을 해야 한다.     7의 배수 판정법(3) 1001이 7의 배수임을 이용 7의 배수인지 판정하는 데는 1001이 7의 배수임을 이용하는 것도 가능하다. 예를 들어,     이므로 123456을 7로 나누는 대신 -123+456 = 333을 7로 나누어 보아도 된다. 이 방법에 따라 1234759680이 7의 배수인지 알아보자. 이 수를 세 자리 끊어 표시하면 1 234 759 680이 되고, 교대로 빼고 더하면, 1 - 234 + 759 - 680 = -154이다. 이 결과는 7의 배수이므로, 원래의 수도 7의 배수임을 알 수 있다. 한편, 1001 = 7×11×13이므로, 7의 배수뿐 아니라, 11과 13의 배수 판정법에도 적용할 수 있다. 즉, 154가 11의 배수이므로 1234759680은 11의 배수이지만, 154가 13의 배수가 아니므로 1234759680은 13의 배수가 아니다.   7의 배수 판정법(4) 라이언스의 방법 이번에는 아주 큰 수에 효과적인 독특한 판정법을 하나 소개하겠다. 이 방법은 뉴욕의 신경정신과 의사인 라이언스(Vosburgh Lyons)가 발견하였다. 역시 1234759680을 예로 들자. 먼저 이 수를 두 자리씩 끊어 표시한다.     이제 각각의 두 자리 수를 7로 나눈 나머지를 차례대로 쓴다.     위의 결과를 오른쪽에서부터 세 개씩 한 조로 묶어 세로로 늘어 놓고 순서대로 더한다.     다시 각 수마다 7로 나눈 나머지를 차례대로 쓴다.     왼쪽 두 숫자, 오른쪽 두 숫자를 묶어 두 수를 만들면 53과 32가 된다. 이 두 수를 7로 나눈 나머지를 구한다.     오른쪽 수에서 왼쪽 수를 빼면 4-4=0이므로 원래의 수는 7의 배수가 된다. 대단히 복잡해 보이지만, 이 방법은 수가 클수록 위력을 발휘하며, 7로 나눈 나머지가 얼마인지까지도 알 수 있다. 화끈하게(?) 1234567891011121314151617181920에 이 판정법을 적용하면 다음과 같다.

 

 

 

 

7의 배수 판정법(5) 토자의 방법 최근에 브라질 상파울루 대학의 토자(Gustavo Gerald Toja)는 라이언스 판정법과 비슷한 판정법을 고안하였다. 이 판정법 역시 판정하려는 수를 두 자리씩 끊고 각각의 두 자리 수를 7로 나눈 나머지를 구하는 것으로 시작한다.                                       라이언스 판정법과 달리, 오른쪽에서 짝수 번째의 수는 7에서 뺀 수로 바꾼다.                                             위의 결과를 거꾸로 쓴다.     새로 만들어진 수를 두 자리씩 끊어 위의 과정을 반복한다.     위의 결과를 거꾸로 쓰고 두 자리씩 끊어 위의 과정을 반복한다.       위의 결과를 다시 거꾸로 쓰면 56이 되고, 이 수는 7의 배수이므로 원래의 수도 7의 배수가 된다.     수학은 사소한 현상을 통해서도 발전한다 요즘처럼 계산기와 컴퓨터가 흔한 세상에 배수 판정법 따위는 큰 의미가 없는 것도 사실이지만, 이런 판정법을 통해 수의 성질과 구조를 이해하는 것은 여전히 의미가 있는 일이다. 예를 들어, 위에서 소개한 두 번째 판정법인 스펜스의 방법이 왜 성립하는지 증명하는 것은 수학과 정수론 시험 문제로 딱 알맞다. 수학은 화려하고 거대한 이론을 통해 발전하기도 하지만, 이처럼 별것 아닌 것처럼 보이는 사소한 현상에 대한 관찰과 연구를 통해서도 발전한다. 여러분도 자신만의 판정법을 한번 찾아보시기를.

 

 

 

글 박부성 / 경남대학교 수학교육과 교수

서울대 수학교육과를 졸업하고, 서울대 수학과에서 석사, 박사 학위를 받았다. 고등과학원 연구원을 거쳐 현재 경남대학교 수학교육과 교수로 재직 중이다. 저서로는 <재미있는 영재들의 수학퍼즐 1,2>와 <천재들의 수학노트>가 있다.

 

원문보기 : http://navercast.naver.com/science/math/1541