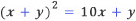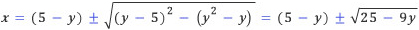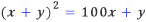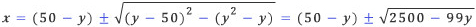[스크랩] 수학의 과학 - 사람이름을 딴 수 '카프리카 수'

수는 어떤 일이나 물건의 개수를 셀 때 많고 적은 결과를 나타내거나, 차례와 위치 등을 표시하는 것이다. 수학에서는 수의 구조를 이해하기 위하여 여러 가지 방법으로 연구하고 있으며, 그 결과 특별한 이름이 붙은 유명한 수가 있다. 여기서는 두 가지 예를 들어 보자.     벨기에 수학자 카탈란의 이름을 딴 카탈란 수 먼저 아래 그림과 같은 정사각형 모양의 도로가 있을 때, 자동차가 대각선 위로는 올라가지 않고 (0,0)을 출발하여 (5,5)로 가는 경우의 수는 몇 가지일까? 이 때 대각선 위로 올라가지 않는다는 것은 아래 오른쪽 그림에서와 같이 (1,0)을 거쳐서 (1,1)로 가거나 (3,0)을 거쳐 (3,1)로는 가는 것은 허용하지만, (0,4)를 거쳐 (2,4)로 가거나 (3,0)을 거쳐 (3,5)로 가는 것은 모두 대각선 위를 지나가게 되기 때문에 허용하지 않는다는 뜻이다. 그림에서 빨간색 화살표는 갈 수 없는 길의 예이고, 파란색 화살표는 갈 수 있는 길의 예이다.

 

 

 

예를 들어 (0,0)에서 (1,1)로 가는 경우는 (0,0) → (1,0) → (1,1)과 같이 가는 한 가지뿐이고, (0,0)에서 (2,2)까지 가는 경우는 다음과 같은 2가지이며, (0,0)에서 (3,3)까지 가는 경우는 5가지이다.     일반적으로 위와 같은 방법으로 (0,0)에서 (n,n)까지 가는 경우의 수는 다음과 같다.     이 수는 이 수를 처음 소개한 벨기에 수학자의 이름을 따서 카탈란 수(Catalan number)라고 한다. 즉, (0,0)을 출발하여 (5,5)로 가는 경우는 다음과 같이 모두 42가지 경우이다.       다각형을 나누는 경우의 수는 카탈란 수를 따른다 카탈란 수는 여러 분야에 활용되고 있으며 특히 수학에서는 아주 많은 분야에서 빈번히 출현한다. 카탈란 수의 대표적인 예는 (n+2)개의 변을 갖는 다각형을 n개의 다각형으로 나누는 경우의 수이다. 이를테면 사각형을 2개의 삼각형으로 나누는 경우의 수는 (0,0)을 출발하여 (2,2)로 가는 경우의 수와 같은 2가지, 오각형을 3개의 삼각형으로 나누는 경우의 수는 (3,3)로 가는 경우의 수와 같은 5가지, 육각형을 4개의 삼각형으로 나누는 경우의 수는 (4,4)로 가는 경우의 수와 같은 14가지이다. 칠각형을 5개의 삼각형으로 나누는 경우의 수는 (5,5)로 가는 경우의 수와 같은 42가지이다.

 

 

 

 

인도의 수학자 카프리카의 이름을 딴 카프리카 수 카탈란 수 이외에도 완전수, 도형수(형상수라고도 함), 친화수(우애수 또는 우정수라고도 함)를 비롯하여 사람의 이름이 붙은 페르마 수, 피보나치 수 등 많은 유명한 수가 있다. 그 중에는 인도의 수학자 카프리카(Kaprika)의 이름이 붙은 ‘카프리카 수’라는 것이 있는데,  카프리카 수는 다음과 같은 유래를 가지고 있다. 인도의 어느 지역에 있는 철도의 선로 옆에는 3025km라고 쓰인 이정표가 있었다. 그런데 어느 날 심한 폭풍우로 이 이정표가 쓰러지면서 두 동강이 났다. 그래서 이정표에 쓰여 있던 3025가 정확히 절반으로 잘려 30과 25로 나누어지게 되었다. 마침 이곳을 지나던 인도의 수학자 카프리카는 쓰러진 이정표의 두 숫자를 보고 재미있는 점을 발견했다. “30+25=55이고 552=3025이네. 이 수는 반으로 나누어 더한 후 제곱하면 원래의 수가 되는구나.” 그 후 사람들은 이와 같은 성질을 갖는 수를 카프리카 수라고 했다.     앞자리 수와 뒷자리 수를 더한 후 제곱하면 원래의 수가 되는 수 일반적으로 짝수 자리 수에서 짝수 자리를 절반으로 나누어 앞자리의 수와 뒷자리의 수를 더한 합을 제곱하면 처음 수가 되는 수를 ‘카프리카 수’ 라고 한다. 가장 간단한 경우인 두 자리 수에서 카프리카 수를 다음과 같은 방법으로 찾아보자. 두 자리 수를 [xy]라고 하자. 이를테면 두 자리 수가 37이라면 x=3, y=7이라는 뜻이다. 이 경우  x는 1부터 9까지의 수 가운데 하나이고, y는 0부터 9까지의 수 가운데 하나이다. 그러면 원래 수는 [xy]=10x+y이다. 이를테면 37=10×3+7이다. 카프리카 수의 성질에 의하여 두 자리 수 [xy]는 다음이 성립한다.     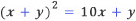즉,     이 식을 만족하는  x를 구하기 위하여 근의 공식에 대입하면 다음을 얻는다.     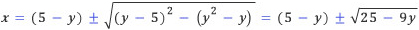여기서 근호 안의 수, 25-9y가 0보다 크거나 같아야 한다. 더욱이 이 수가 완전제곱수이어야 x가 자연수가 된다. 첫째 조건에서 y는 3보다 작아야 하니, 1 혹은 2이다. 두 번째 조건에서 y에 2를 대입하면 25-9y = 7이 되니 y는 1밖에 없다. 즉 25-9y는 16이고, x는 8 혹은 0이 된다. x는 0이 될 수 없으므로 x=8가 유일한 답이다. 즉, 두 자리수인 카프리카 수는 81뿐이다. 실제로 81은 8+1=9이고 92=81이다.     두 자리의 카프리카 수는 1개뿐, 네 자리의 카프리카 수는 3개 뿐 이번에는 네 자리 수 가운데 카프리카 수를 구하여 보자.  네 자리 수를 [abcd]라 하면, 이 수는 다음과 같이 나타낼 수 있다. (a는 1에서 9까지의 정수이고 b,c,d는 0에서 9까지의 정수임)     이 네 자리 수 [abcd]를 두 자리의 카프리카 수를 구할 때와 마찬가지로 [xy]로 나누면 x=10a+b, y=10c+d이다. 그러면 카프리카 수의 성질에 의하여 다음이 성립한다.      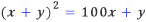즉,      이 식을 만족하는 x를 구하기 위하여 근의 공식에 대입하면 다음을 얻는다.     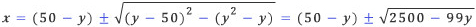두 자리의 경우와 마찬가지로 2500-99y는 0보다 크거나 같아야 하고, 완전제곱수이어야  x가 자연수가 된다. 첫 번째 조건에서 y는 1부터 25 사이의 자연수라는 것을 알 수 있다. 그 중 두 번째 조건을 만족시키는 y는 1과 25밖에 없다    따라서 y가 1일 때 x를 계산하면 0 또는 98이 되고, y=1이므로 원하는 네 자리 수는 0001 혹은 9801이다. 그러나 0001은 네 자리수가 아니니 첫 번째로 얻은 네 자리 카프리카 수는 9801이다. Y가 25일 때 x를 계산하면 20혹은 30이 나온다. 따라서 2025와 3025가 카프리카 수라는 것을 알 수 있다.  확인 삼아 9801, 2025, 3025는 각각 다음과 같이 카프리카 수라는 것을 알 수 있다.     실제로 네 자리의 수 가운데 위의 세 수 9801, 2025, 3025만이 카프리카 수이다.     6자리의 카프리카 수 77772=60481729 이와 같은 방법으로 6자리의 수 가운데에서도 카프리카 수를 찾을 수 있다. 특히 미국의 헌터(J. A. H. Hunter)는 8자리의 카프리카 수를 찾았는데, 그 수는 60481729이다. 이 수는 다음과 같음을 알 수 있다.     앞에서 예를 든 카탈란 수는 다양한 분야에서 활용되는 수이며, 카프리카 수는 수학적으로 흥미로운 수이다. 여러분도 수학공부를 열심히 하면 여러분의 이름이 붙은 수를 만들어낼 수도 있지 않을까?

 

 

 

글 이광연 / 한서대학교 수학과 교수

성균관대학교 수학과를 졸업하고 와이오밍 대학교에서 박사후 과정을 밟았다. 저서로는 <웃기는 수학이지 뭐야>, <수학자들의 전쟁>, 2008년 문화체육관광부 우수과학도서로 선정된 <수학블로그> 등이 있다.

 

원문보기 : http://navercast.naver.com/science/math/1623